It seems I have been living under a rock when it comes to what appears to be a fundamental tool in DJing (a side hobby of mine)
It’s called Harmonic Mixing which is the implementation of the Circle of fifths found in music theory.
This post is about my first foray into harmonic mixing & how I can improve my DJing by incorporating the skills into my toolbox.
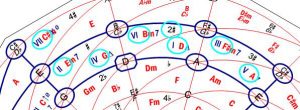
The underlying principle is that certain keys harmonise with one another. This is a useful asset for DJs looking to produce a smooth flowing set where each track appears to “sing” with the next.
Mark Davis created the Camelot Wheel to help visualise which keys harmonise together (based on the circle of fifths). Here is a representation of the Camelot Wheel I use (because I use Traktor software & hardware).
If you want more detailed info on the technique, check out the resource links at the bottom of this page.
The Experiment
The hypothesis was that using the Camelot wheel to structure my set would lead to a better flow of tracks & ultimately take the listener on an audio “journey”…
For my experiment I had 3 rules:
- Each track has to be the same or +1 key from the current track (i.e. move around the wheel in a clockwise direction)
- Harmonise as much as possible! Make those mixes sing!
- I had to enjoy producing the mix
The Results
Conclusions
- The mix hung together & flowed much better than my previous mixes
- I discovered some of the boundaries of harmonic mixing
- There’s still a balance of when to mix tracks & when to not
- Making “space” for each track is still essential
- Some tracks were not actually harmonised even though the tool said they were
- Even if the tracks are harmonised, the flow of the mix can be interrupted by abrupt transitions & poor levelling (i.e. lacking DJ skill)
- Letting keys dictate the structure of my set lead me to play tracks of several genres & rhythms in a different order to what I would normally play them in
- This makes the mix still “wander” more than I like it, but it’s certainly less noticeable than clashing keys!
Next Experiments
- Anti-clockwise around the wheel
- Switching from minor to major (& vice-versa)
Useful resources
Music stack exchange
Mixed In Key